Research

Research in Solid State Dynamics

Despite the existence of international conventions such as the Anti-Personnel Mine Ban Convention (Ottawa Convention), the Convention on Cluster Munitions, and the Convention on Certain Conventional Weapons, the annual number of casualties caused by mines and unexploded ammunition remains at 5800. Moreover, the presence of undetected mines and ammunition creates obstacles for the local population, preventing them from farming on previously fertile land and hindering their ability to return home after conflicts (source: external pagehttps://www.gichd.orgcall_made).
With our combined expertise in magnetism and electronics design, we are dedicated to developing innovative tools for humanitarian demining. Our approach involves a novel technique capable of discerning the size of buried metal objects, combined with advanced signal processing utilizing field-programmable gate arrays (FPGAs). By implementing this approach, we aim to significantly enhance the efficiency of the search process.
We are offering a semester or master thesis opportunity within this project. No specialized prior knowledge is required, although the lecture "Electronics for Physicists II (Digital)" would be beneficial in supplementing the topic. Throughout the project, you will gain familiarity with circuit design, hardware description languages employed for programming FPGAs, and the interaction between magnetic fields, various metals, and soil. The acquired skills in electronics design will prove highly valuable across various disciplines of experimental physics.
Contact: Dr. Yves Acremann
In solid state physics we usually assume that the lattice, the electron gas as well as the spin system are in thermal equilibrium: A single local temperature is sufficient to describe the state of the solid. This changed with the development of ultrafast lasers delivering sub-picosecond pulses: If we expose a metal to a femtosecond laser pulse the energy is mainly absorbed by the electron gas. Energy is then subsequently transported to the lattice as well as the spin system, driving the electron gas, lattice and spin system out of equilibrium.
The spin system is even more complex as not only energy needs to be transported away, but also spin angular momentum. This process is still not fully understood and is therefore of fundamental interest. One of the spin transfer processes is governed by the generation of a spin polarized current. This enables us to study spin spin transport phenomena on the femtosecond time scale.
Laser-induced demagnetization is also of technological interest for magnetic recording devices: in order to optimize hard disks for fast writing times, long data retention times, and high storage densities, conventional writing needs to be combined with pulsed laser heating. The heat assisted magnetic recording (HAMR) technique therefore combines a magnetic field source with a pulsed laser diode to heat up the magnetic bit during writing.
Development of an imaging spin detector
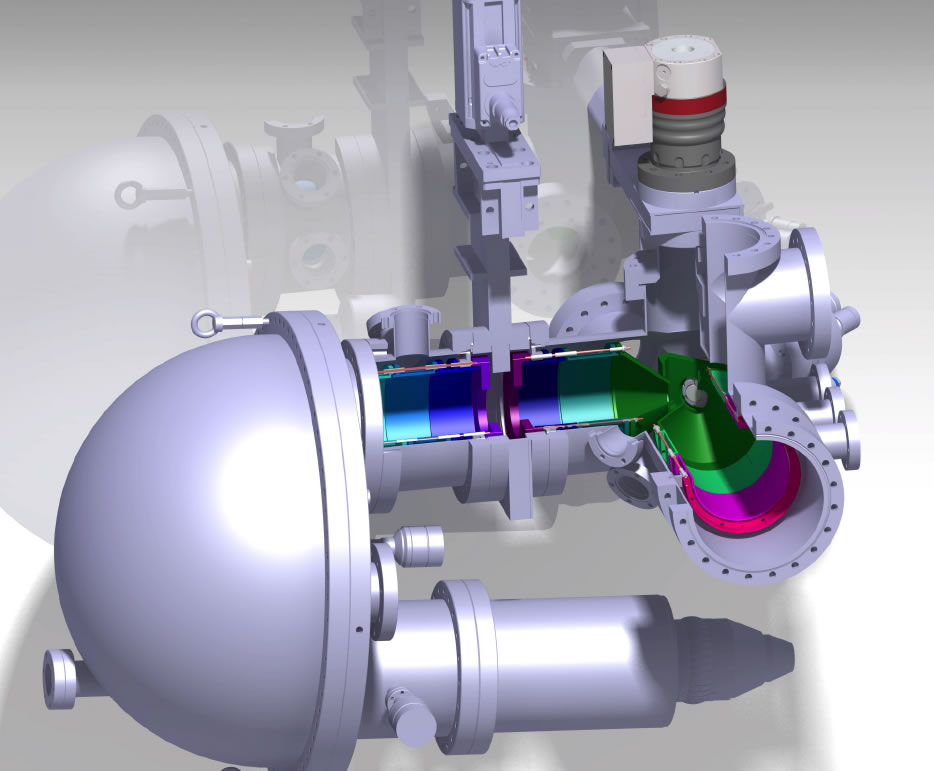
We developed a novel spin detector based on low energy scattering of spin polarized electrons on a Iridium crystal. The detector has been developed together with the group of external pageProf. Schönhensecall_made (University of Mainz, Germany).
Electrons from the output of a hemispherical energy analyzer are elastically scattered on a an Iridium surface (Figure 1). Due to the spin-orbit coupling within Ir, the reflectivity is spin dependent and therefore acts as a spin filter. As the scattering process is elastic, the imaging properties of the hemispherical analyzer can be preserved, allowing for parallel detection of electron energy and emission angle. Therefore, the efficiency of this detector is significantly better compared to a traditional Mott spin detector. This detector has been designed by our group, and has been manufactured by the physics machine shop. We use it routinely for time-resolved photoelectron spectroscopy.
Spin dynamics within the electron gas
Using our spin and time-resolved photoelectron spectrometer we can observe the laser-induced ultrafast demagnetization effect of iron within the electron gas and can distinguish electrons of different binding energies. The Spin polarization as a function of the binding energy and time is shown in figure 2.
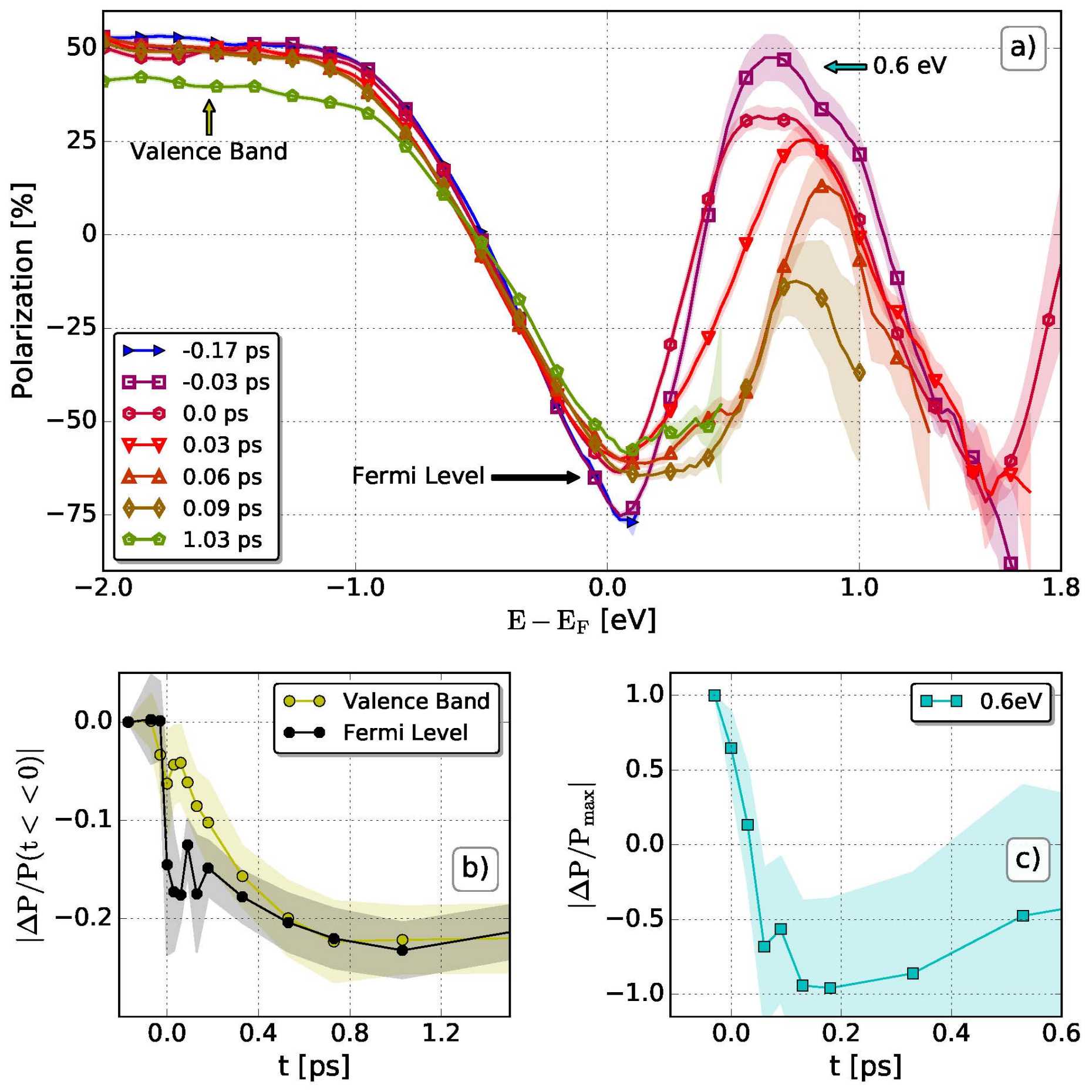
At the Fermi energy, the spin polarization is negative as the polarization is dominated by minority electrons. At deeper in the valence band the spin polarization is dominated by majority electrons. Right after the laser pulse we observe non-thermal electrons populating states above the Fermi edge. These possess the polarization of the states they originate from. As the electron gas thermalizes the spin polarization at the Fermi energy is reduced. Surprisingly, the spin polarization within the valence band requires approx. 400fs for depolarization.
This experiment shows, that the spin system does not react in a uniform way to the pump pulse, but shows internal dynamics. Therefore, on the femtosecond time scale, the magnetization separates into different parts similar to how the single temperature paradigm changed with the development of ultrafast lasers.
Spin transport dynamics
The ultrafast demagnetization effect allows for the generation of femtosecond spin current pulses, which is expected to extend the fields of spin transport and spintronics to the femtosecond time domain (external pageBattiato et al., Phys. Rev. Lett. 105, 027203 (2010)call_made). Thus far, directly observing spin polarization has not been possible. Using our spin and time resolved photoelectron spectrometer it has become possible to directly observe the spin injection from a ferromagnet into a gold layer.
The setup is shown in figure 3: The ferromagnet is excited through the transparent substrate. The temperature gradient within the Fe film causes the generation of a spin current pulse. The spin injection into the Au film can be observed by spin-resolved photoelectron spectroscopy.
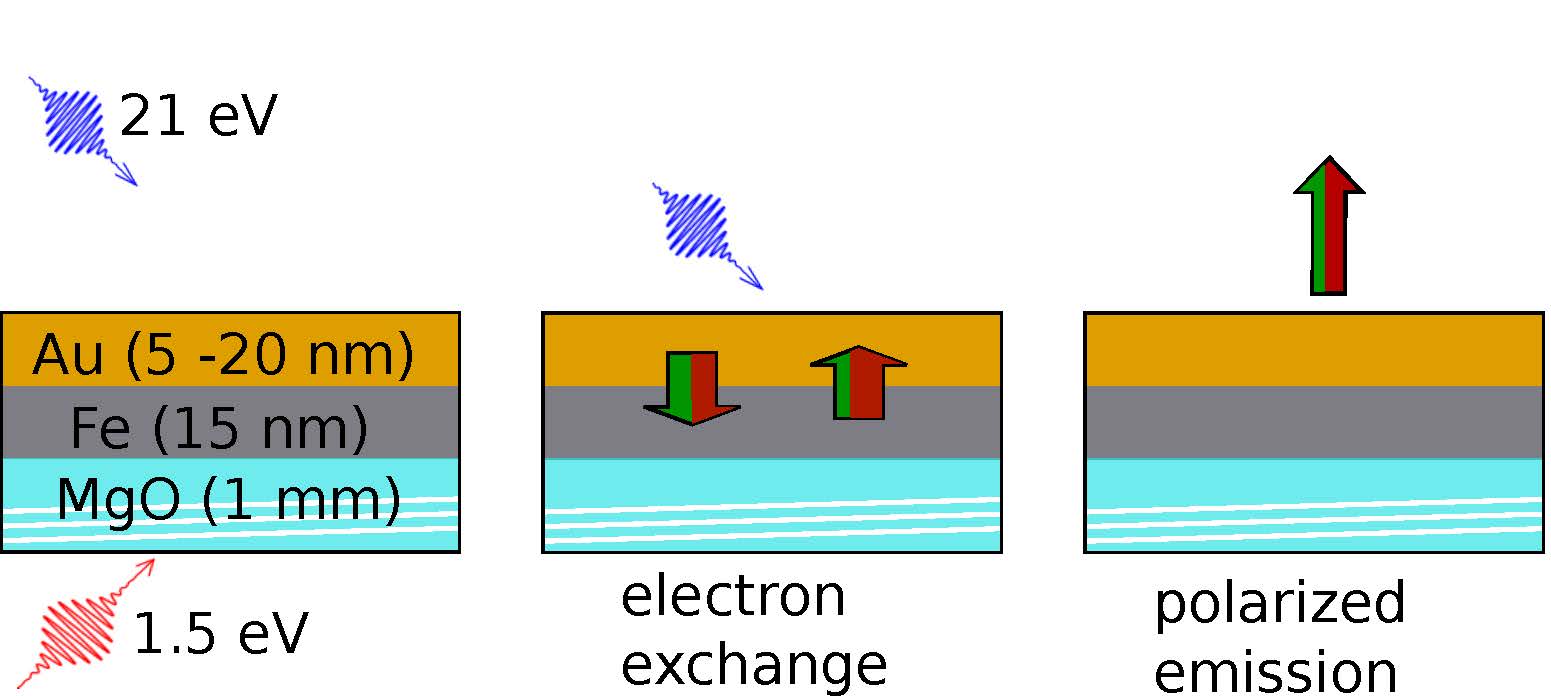
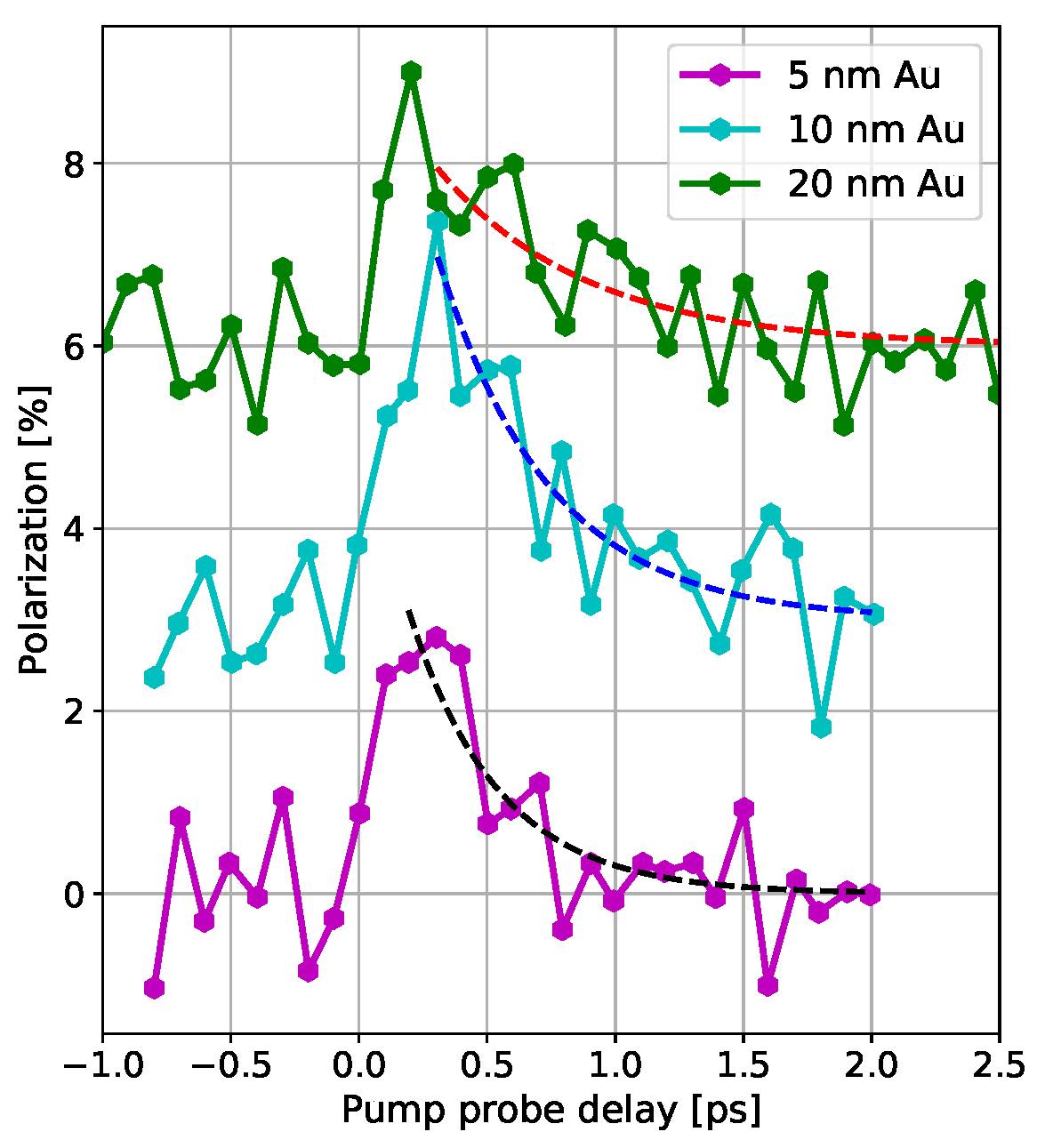
Figure 4 shows the results: The spin polarization on the Au layer surface can be detected by our instrument, although the spin polarization is only a few percent. The decay depends on the Au layer thickness. This is an important result as it indicates, that the decay is a transport- or interface effect. The storage of spin angular momentum in the Au layer and its transport to the interface is only visible in time resolved experiments and can not be observed in classical spin transport experiments.
We are currently developing techniques for extending electron microscopy to the time domain. We follow two avenues:
Time-resolved scanning electron microscopy
In this project we intend to modify an existing scanning electron microscope by adding a laser to the electron source. The goal for this instrument is to study picosecond dynamics in semiconductor devices at the nanometer length scale. The laser will launch electron pulses from a photocathode, which are accelerated and focused onto the sample. This electron beam is scanned over the sample surface while the secondary electron spectrum is measured. By measuring the energy spectrum of the secondary electrons emitted from the sample, one can detect the local electric potential. The pulsed nature of the probe beam will offer a temporal resolution of a few picoseconds. This instrument is currently under development.
Transmission electron microscopy combined with a time-resolved electron detector
In collaboration with external pageProf. Rafal Dunin-Borkowskicall_made from the Forschlungszentrum Jülich (Germany) we are using the temporal resolution of a delayline detector in combination with a high performance transmission electron microscope to achieve imaging with a temporal resolution of 100ps. It will enable us to study magnetic memory devices in operando.
Research in Physics Education
Acquiring deep conceptual knowledge is a central goal of physics education. However, research in the last decades at upper secondary school and introductory college level has shown that a substantial amount of students has major difficulties to understand physics concepts even though many students are able to successfully apply problem-solving algorithms to traditional quantitative problems.
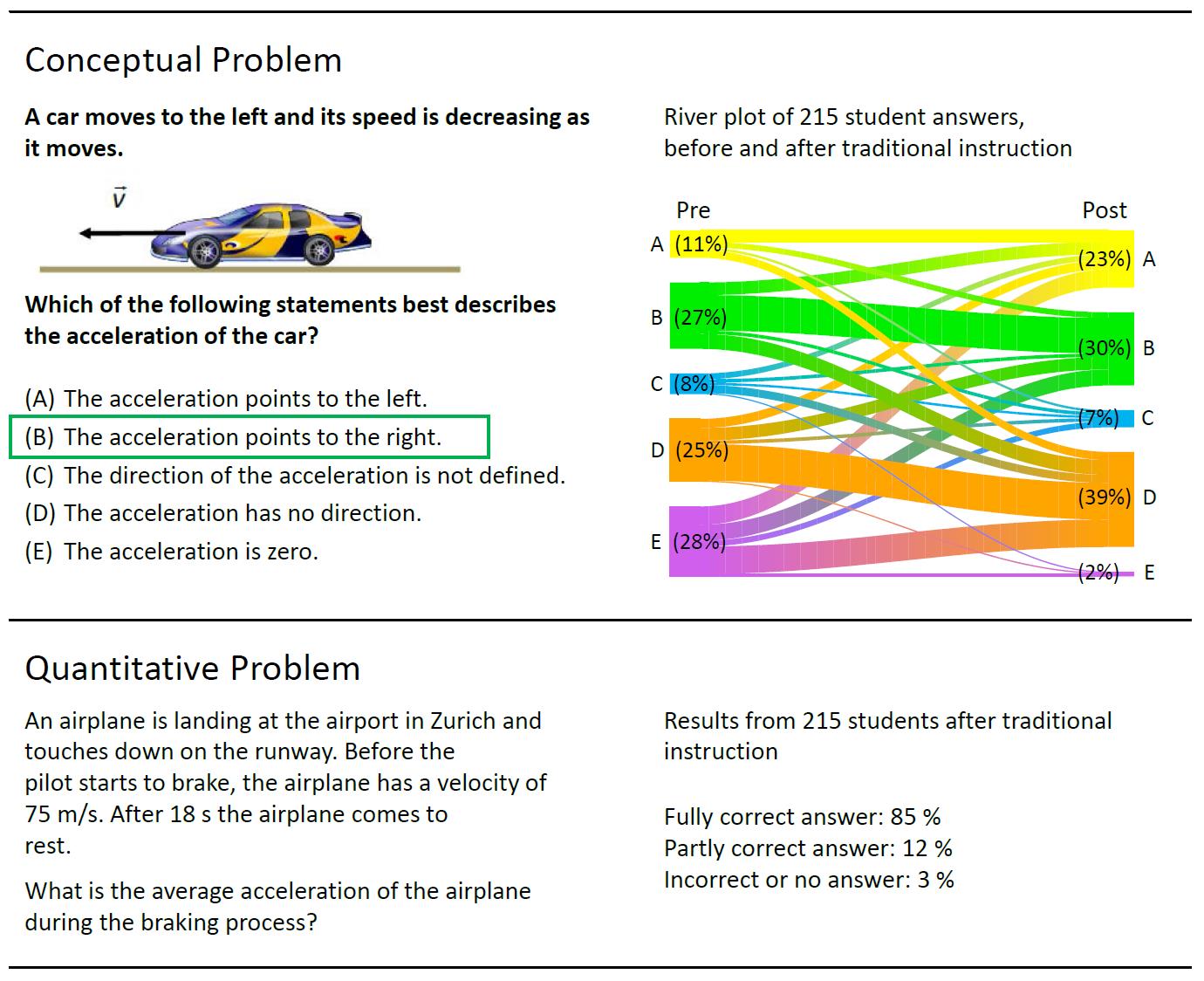
The following figure exemplarily illustrates these findings with student answers to two problems applied in our formative assessment study (Figure 1). While a majority of students is able to solve a quantitative problem after traditional instruction, the conceptual understanding has not improved.
In educational research, we pursue projects which focus on promoting concept learning in physics instruction at Swiss Gymnasiums.
Formative Assessment to Foster Concept Learning
A promising method to enhance concept learning is formative assessment. It makes learning visible by employing a feedback system that continuously provides information about students’ learning progress to both teachers and students. Teachers can then use this feedback to adjust their instructions in order to better meet the needs of the students, while students can assess their level of understanding regarding the learning goals and thereby identify what they still need to work on.
In cooperation with the group of Prof. Elsbeth Stern at D-GESS, we conducted a study to investigate the effect of formative assessment on conceptual learning in physics at Gymnasium level in Switzerland. Twenty-nine teachers and 604 students from the German speaking part of Switzerland participated in a cluster randomized field trial with active control. After one day of training, teachers in the experimental group applied formative assessment in a 14-lessons course about kinematics. Results show that, after controlling for prior knowledge, intelligence, and gender, students exposed to the formative assessment intervention performed significantly better in tasks on conceptual understanding than students who underwent traditional teaching. Moreover, the formative assessment classes’ better conceptual understanding was not at the expense of their quantitative problem-solving performance.
Investigating Conceptual Understanding in Kinematics
In order to evaluate the conceptual knowledge of students in the formative assessment study, we have developed a kinematics concept test. The test consists of 49 multiple-choice items which are based on seven kinematics concept and makes use of three representations (pictures, graphs, tables).
A structural analysis of the test results of 664 Swiss Gymnasium students revealed that students’ knowledge structure in kinematics seems to be mainly based on the mathematical concepts of rate, vector, and area under the curve. Still, also the physics concepts are present in a more fine-grained substructure. Moreover, we found that students have difficulties to transfer a concept from one representation to another.
In the formative assessment study, we used kinematics concept questions to induce peer discussions in small groups of about three students. In order to comprehend students’ problem-solving processes, we are currently analyzing audio recordings of these student group discussions.
In a collaboration with the group of external pageProf. Jochen Kuhncall_made at TU Kaiserslautern, we further investigate problem-solving processes using eye-tracking technology. By recording students’ visual attention and eye saccadic movements while they solve concept questions, we aim to gain deeper insight into their cognitive activities.
Technology-Enhanced Active Learning
Many studies have shown clear advantages of active learning over direct instruction for acquiring deep conceptual knowledge. Currently, digitization is entering the classroom. New technologies offer new approaches for active and collaborative learning in science. In a recently launched project, we aim to explore the potential of virtual and augmented reality in physics education.
In our first implementation of virtual reality, we address students’ difficulties understanding the relation between electric field and potential. Students’ problems are often conceptual in nature and can be related to non-existing conceptual mental models. We offer a learning setting where the relation between potential and vector field can be explored and consolidated in a playful and active way. Wearing a Microsoft HoloLens, students move through a visualized three-dimensional potential‐landscape and identify which one of a given set of vector fields corresponds to the virtual landscape.
A second implementation of augmented reality with a focus on inquiry learning is currently being planned. As augmented reality integrates virtual and physical components in real-time, this technology makes it possible to integrate prompts as scaffolds during experimentation and to simultaneously use different representations of the measured data. We want to investigate how scaffolding and using multiple representations within the augmented reality setting affect learning processes.
Concreteness Fading
Electromagnetism, and particularly Faraday’s law are central topics in high school and university. Yet, the abstractness and the relational structure of electromagnetic phenomena make this content difficult to learn. One instructional approach suggested to support learning of abstract content is the so-called concreteness fading approach in which students start with concrete representations (e.g. three apples) that subsequently «fade» towards more idealised ones (e.g., three dots representing apples).
Concreteness fading exemplifies the virtues of step-wise sequencing of multiple representations and it has been suggested as a general instructional approach. While it has received some promising empirical support, others have advocated starting with the more idealised representations before moving to the concrete ones (i.e., concreteness introduction). However, studies about concreteness fading have rarely been conducted at upper secondary or university level.
In a collaboration with external pageProf. Lennart Schalkcall_made (PH Schwyz) and external pageDr. Tommi Kokkonencall_made (University of Helsink), we investigate concreteness fading as instructional approach to learn Faraday’s law. An experimental pilot study with 74 Finish students at high school level gave indications that there is no difference between concreteness fading and concreteness introduction regarding students’ learning gains. A larger study including 200 students at secondary school level in Switzerland and Finland is going to be conducted in 2020.
